Binárny vyhľadávací strom

Riešenia

Úloha 20

V prvej vrstve môže by najviac 1 vrchol, v druhej vrstve najviac 2 vrcholy, v tretej vrstve najviac 4 vrcholy atď. Všeobecne na i-tej vrstve môže by najviac 2^i-1 vrcholov.

Ak h = 0, tak obsahuje 1 prvok. Ak h = 1 , tak počet vrcholov je súčtom vrcholov z prvej a druhej vrstvy t.j. 1 + 2¹ = 3 atď. Všeobecne pre strom výšky h určíme maximálny počet vrcholov ako súčet počtov vrcholov vo vrstvách 1 až h + 1:

N = 2^{h + 1} - 1

Úloha 21

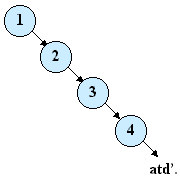Ak sú vstupné hodnoty, z ktorých vytvárame binárny vyhľadávací strom už usporiadané (napr. vzostupne), tak bude zrejme každý ďalší prvok pripojený ako pravý syn predchádzajúceho a výsledný strom tak bude úplne degenerovaný - pripomína skôr lineárny zoznam! Ide o najhorší prípad.

   Vo všeobecnosti dopredu vôbec nevieme, aký bude ma binárny vyhľadávací strom tvar, ako sa bude "rozrasta". Môže sa sta, že sa vytvorí degenerovaný strom (najhorší prípad). Vyhľadávanie v takomto strome vyžaduje rádovo O(n) porovnaní, čo je pre prax nepoužiteľné (pomalé !).

Ideálne by bolo, keby bol binárny vyhľadávací strom dokonale vyvážený. Vtedy sa dosahuje pri vyhľadávaní za ideálnych podmienok rýchlos rádovo O(log₂n). Ideálnymi podmienkami rozumieme, že vyhľadávací strom zostane stále dokonale vyvážený. To si však vyžaduje používa dokonalejšie funkcie na vkladanie  a rušenie vrcholov.

Pri vytváraní vyhľadávacieho stromu sa môžeme spolieha na náhodu a predpoklada, že strom nebude priveľmi nevyvážený. Dá sa ukáza, že priemerná výška binárneho vyhľadávacieho stromu s n vrcholmi je približne 1,4·log₂n, čo sa príliš od ideálneho prípadu nelíši.